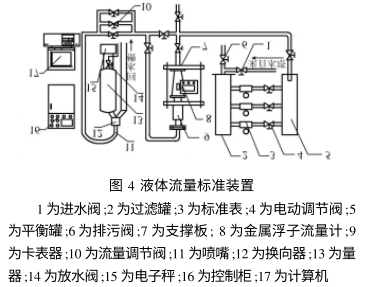
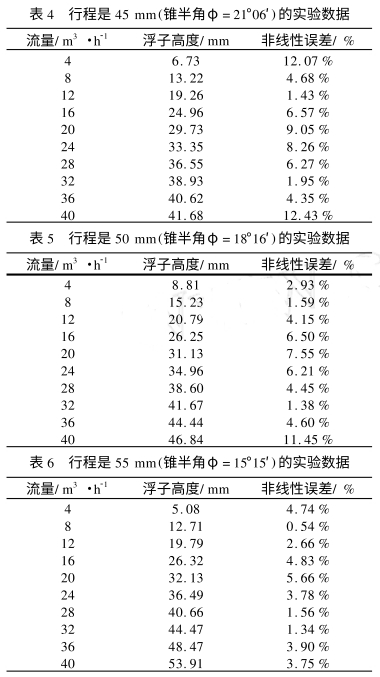
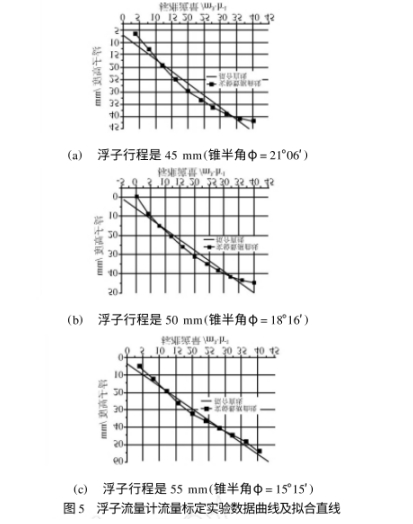
| <tr id='y8272'><strong id='y8272'></strong><small id='y8272'></small><button id='y8272'></button><li id='y8272'><noscript id='y8272'><big id='y8272'></big><dt id='y8272'></dt></noscript></li></tr><ol id='y8272'><option id='y8272'><table id='y8272'><blockquote id='y8272'><tbody id='y8272'></tbody></blockquote></table></option></ol><u id='y8272'></u><kbd id='y8272'><kbd id='y8272'></kbd></kbd> |